
Looking at G*Power's documentation, they use a method based on Hsieh, Bloch, & Larsen (1998). In that vein, it may help you to read my answer here: Simulation of logistic regression power analysis - designed experiments. It further matters what the correlation between $x_2$ and $x_1$ is: The more correlated they are, the more data would be required to achieve the same power.Īs a result of these facts, the way I try to calculate the power in these more complicated situations is to simulate. It matters how $x_2$ is distributed: The more widely spread the values are, the more powerful your test, even if the odds ratio is held constant.
In addition, the effect (e.g., odds ratio) of the added variable, $x_2$, isn't sufficient to determine your power to detect that effect. You can get a list of some at UCLA's statistics help website here. Instead there are many different "pseudo-$R^2$s" that may be similar to the $R^2$ from a linear model in different ways. The problem is that there isn't really a $R^2$ for logistic regression. Reading the tutorial in 27.4 from the software manual makes no variation of $R^2$, whereas this example, does not discuss the improvements made from $R^2$. But I am not sure what to set R² other X equal to.
Calculating gpower for a logistic regression how to#
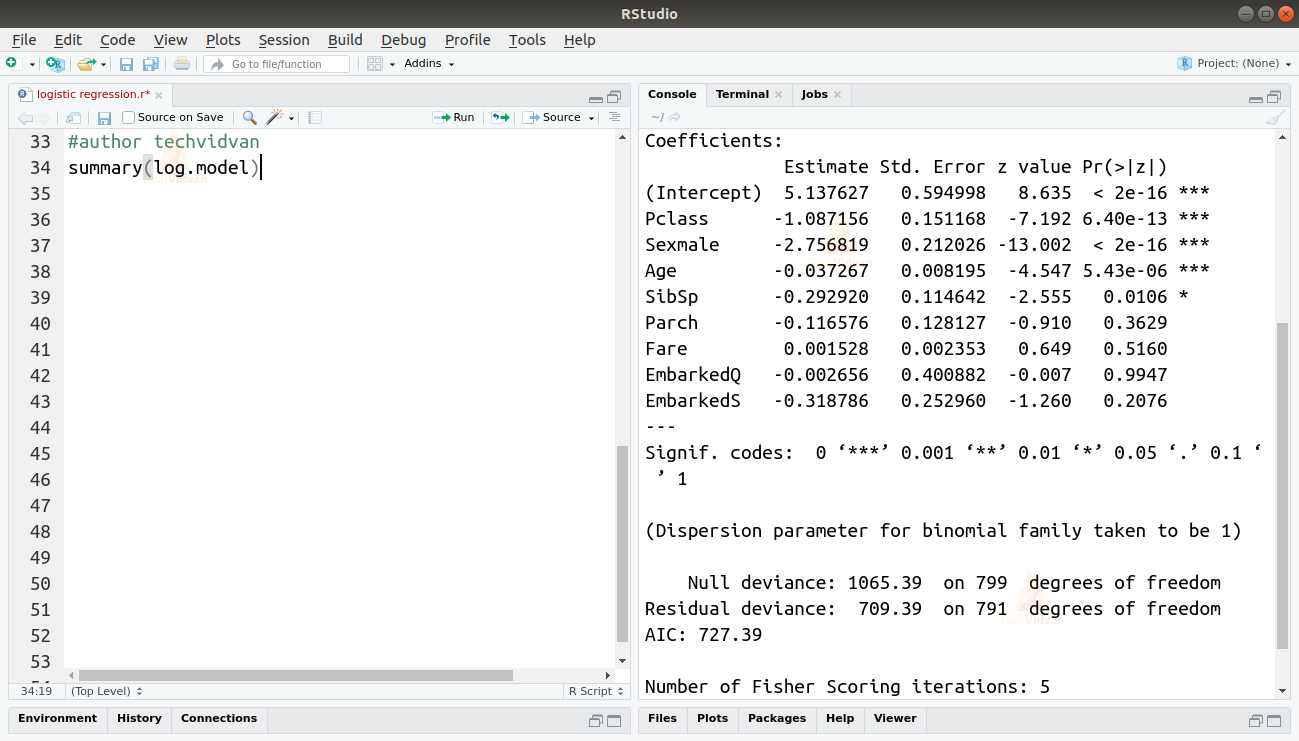
I don't know how to do a more detailed power analysis for multiple logistic regression.įrom what I understand, in G*Power I set Test Family = z tests and statistical test = logisitic regression. I want to do something similar for a logistic regression using G*Power.īut there appears to be very little documentation on multiple logistic regression models like my situation. I have found an example for linear regression that uses an $F$-Test. When I run an ANOVA test, I see no significant improvement in the second model, but I want to assess the power associated with including the additional variable in model 2. I can output a new $R^2$ value associated with the second model. I then go and add another predictor variable to fit a second model.
I have a logistic regression model and output an $R^2$ value.


 0 kommentar(er)
0 kommentar(er)
